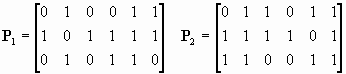ERRATA

ERRATA

Shipley, B. (2000). Cause and Correlation in Biology. A user’s guide to path analysis, structural equations and causal inference. Cambridge University Press.

Updated March 28, 2002. Please inform me (bshipley@courrier.usherb.ca) of any other errors.

Page 24

Replace the following sentence (last paragraph):

… I develop a translation device to move between causal models and observations (statistical) models.

With the following sentence:

… I develop a translation device to move between causal models and observational (statistical) models.

Page 28:

Replace the following sentence:

… the natural state of a non-collider is the active (ON) state and the natural state of a non-collider is the inactive (OFF) state.

With the following sentence:

… the natural state of a non-collider is the active (ON) state and the natural state of a collider is the inactive (OFF) state.

Page 31:

Table 2.1. Replace the following sentence:

I(X,{U,W},Y).

With the following sentence:

~I(X,{U,W},Y).

Page 33:

Replace the following sentence:

If (X,F ,Y) then P(X,Y)=P(X)xP(Y)

With the following sentence:

If I(X,F ,Y) then P(X,Y)=P(X)xP(Y)

Page 48:

Replace the following sentence (last paragraph):

… it is useful briefly to look at what philosophers of science…

With the following sentence:

… it is useful to briefly look at what philosophers of science…

Page 72:

Replace the following sentence:

… {(A,C), (A,D), (A,E), (A,F), (B,E), (B,F), (C,D), (C,F), (D,F), (E,F)}.

With the following sentence:

… {(A,C), (A,D), (A,E), (A,F), (B,E), (B,F), (C,D), (C,F), (D,F)}.

Page 73:

Table 3.1 Delete the last line (beginning with E,F) of this table

Page 80:

Replace the following sentence (last paragraph):

The middle graph show the same complicated non-linear function in the range 1 to 3 of the X values and the middle graph shows this in the range 1.5 to 2.5 of the X values.

With the following sentence:

The middle graph shows the same complicated non-linear function in the range 1 to 3 of the X values and the graph to the right shows this in the range 1.5 to 2.5 of the X values.

Page 105:

Replace the following equations:

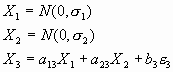
With the following equations:

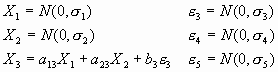
Page 113:

Replace the following sentence (last paragraph):

… which we group together in a vector , we will write the population covariance matrix as .

With the following sentence:

… which we group together in a vector , we will write the model covariance matrix as .

Page 115:

Replace the following formula:

With the following formula:

Page 128:

Replace the following table heading:

Table 4.5. Decomposition of the total association between each pair of variables in Figure 4.5 into direct effect,…

With the following table heading:

Table 4.5. Decomposition of the total association between each pair of variables in Figure 4.7 into direct effect,…

Page 156:

Replace the following sentence (first paragraph):

… answered ‘[c]oncepts have the same reality of lack or reality as other ideas…

With the following sentence:

… answered ‘[c]oncepts have the same reality or lack of reality as other ideas…

Page 169-171 (Box 6.1):

Replace the text in this box by the following: Note that the IDEN program uses the correct formulation (below) of the FC1 rule for structural identification of a measurement model.

The FC1 ("Factor Complexity 1") rule for the structural identification of a measurement model assumes that each observed indicator variable is caused by only 1 latent variable (hence its name).

For each latent variable, L_i, in the measurement model, construct a binary matrix P_i with q_i rows and t columns; q_i is the number of observed indicator variable of L_i and t is the total number of observed indicator variables in the model. Each element (p_ij) of P_i has a 1 if the error variables of indicators i and j are d-separated or if the covariance between then has been fixed and if the covariance of the latents associated with indicator variables i and j are free.

Form the matrix D_i=P_iP’_i. Iteratively multiply until you get the matrix .

The first requirement for structural identification is that every element of be non-zero in the row corresponding to the indicator of L_i that defines its scale. This must be true for all latent variables in the model.

The second requirement for structural identification of the full measurement model is that, for every pair of latent variables whose covariance is to be estimated (i.e. that are not d-separated or whose covariance is not fixed) there must be at least one pair of indicator variables (one for each latent) whose error variables are independent (i.e. d-separated) or whose covariance is fixed.

The third requirement for structural identification of the full measurement model is that, for every latent variable whose variance is to estimated (i.e. is not fixed), there must be at least one pair of indicator variables (one for each latent) whose error variables are independent (i.e. d-separated) or whose covariance is fixed.

I will now show how this rule works with reference to Figure 6.3.

In this model there are two latent variables, so we need two P matrices:

Note that p₁₂=p₂₁=1 in P₁ because e ₁has a fixed (zero) covariance with e ₂ and similarly for e ₄ and e ₅ in P₂. There are three indicator variables for each latent and so q₁=q₂=3. We must form and . These are the same in this example, although this is not true in general:

.

Now, the first requirement is that every element in the row of each matrix representing the scaling variable must be non-zero. The scaling variable of the first latent variable is X₁ and so every element in row 1 of the first matrix must be non-zero. The first part of this first requirement is fulfilled. The scaling variable of the second latent variable is X₄ and so every element in row 1 of the second matrix must be non-zero. The second part of this first requirement is also fulfilled.

The next requirement is that there be at least one pair of error variables (one associated with an indicator of each unique pair of latents) whose covariance is zero or fixed to some other value. Error variables e ₂ and e ₅ fulfill this second requirement.

The final requirement is that there must be at least one pair of error variables (associated with an indicator of each latent) whose covariance is zero or fixed to some other value. Error variables e ₁ and e ₂ fulfill this requirement for the first latent variable and error variables e ₄ and e ₅ fulfill this requirement for the second latent variable. Therefore this measurement model is structurally identified.

Page 177, bottom of last full paragraph:

Replace the following text:

" Since these simulated data sets are mutually independent and large in number you can obtain a 95% confidence interval (Manly 1997) around p by referring to a normal distribution whose mean is (x-Np) and whose standard deviation is Np(1-p). Thus the 95% confidence interval is p± 1.96Np(1-p)."

With the following text:

" Since these simulated data sets are mutually independent and large in number you can obtain a 95% confidence interval (Manly 1997) around p by referring to a normal distribution whose mean is x and whose variance is Np(1-p). Thus the 95% confidence interval is ."

Page 178:

Replace the following text:

Given a desired degrees of freedom (df) find a value for v such that d£ v(v+1)/2 and d³ v(v-1)/2. Call this v^*. For instance, if we want df=9 then choose v*=4 since v(v-1)/2=6 and v(v+1)/2=10.

Calculate c=df=v^*. So, if we want df=9 then c=9-6=3.

With the following text:

Given the desired degrees of freedom (df), find the smallest integer value of v such that df£ v(v+1)/2. This will be the smallest integer value of v such that . For example, if df=9 then we need the smallest integer value of v such that . Thus v=4.